

本福特定律(第一数字定律)详解
本福特定律在线测试,https://www.itshenji.com/benfute
本福特(Benford)定律又称第一数字定律,它是数字统计的一种内在规律,指所有自然随机变量,只要样本空间足够大,首位1-9的数字出现的概率在一定范围内具有稳定性,即以1开头的样本占样本总量的30.1%,以2开头的样本占样本总量的17.6%,而以9开头的样本始终只占5%左右(如下图)。
常用于检查各种数据是否有舞弊、造假。
举一个例子
某银行有1000多个储蓄账户,存款金额不等。这些数字的第一位 (非零) 有效数字可能是1到9之间的任何一个。现在,我们设想一下,在上千个存款数据中,第一位数字是1的概率有多大?
大部分人可能很快地回答:应该是1/9吧。因为从1到9,9个数字排在第一位的概率是相等的,每一个数字出现的概率都是1/9,大约11%左右。
这种看似十分正常的思维却与真实的规律相悖。
经研究发现,很多情况下,首位数字是1的概率要比靠直觉预料的11%大得多。数字越大,出现在第一位的概率就越小,数字9出现于第一位的概率只有4.5%左右。各个数字出现在首位的概率遵循图1左图所示的概率分布。从图中可以看出,首位数字为1的概率可达30.1030%,而首位数字为9的概率仅为4.5757%。
这就是本福特定律。
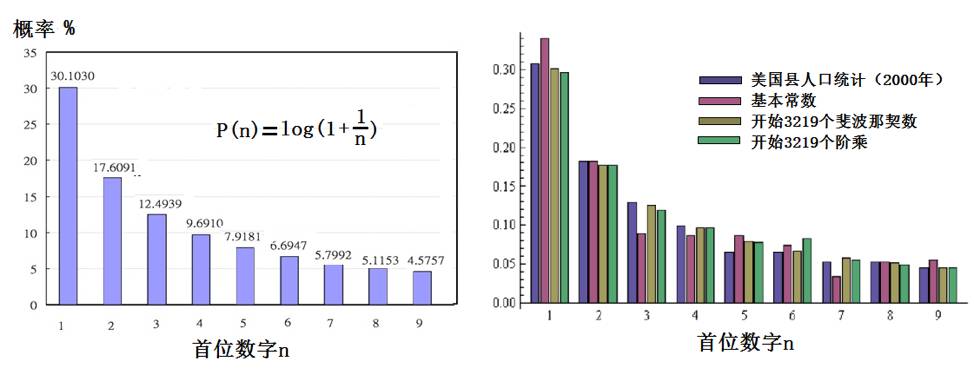
图1:本福特定律(首位数定律)
事实上,本福特定律的发现者并不是本福特,而是美国天文学家西蒙·纽康 (Simon Newcomb,1835 - 1909) 。
纽康在查阅对数表(常用对数编排而成的表格,用以计算)时发现了一个奇怪的现象:包含以1开头的数的那几页比其他页破烂得多,似乎表明计算所用的数值中,首位数是1的概率更高,因此他在1881年发表了一篇文章提到并分析了这个现象,但没有引起人们的注意,直到57年之后的1938年,本福特又重新发现这个现象。
说来令人奇怪,科学定律的发现有时候来自于一些毫不起眼、小得不能再小的现象,本福特的发现便是如此。“以1开头的数字比较多”,这也算是一个定律吗?
本福特发现这种现象不仅仅存在于对数表中,也存在于其它多种数据中,于是,本福特检查了大量数据而证实了这点。
本福特和纽康都从数据中总结出首位数字为n的概率公式是:
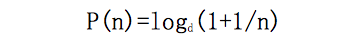
其中d取决于数据使用的进位制,对十进制数据而言,d=10。
随后,本福特收集并研究了20229个统计数据,包括河流面积、人口统计、分子及原子重量、物理常数等多种来源的资料,并分成20组。数据来源虽然千差万别,却基本上符合本福特定律,见图2所示的数据表。表中最后一行的数值,是根据本福特概率公式计算得到的每个数字出现于首位的概率,读者可以将它与真实数据相比较。
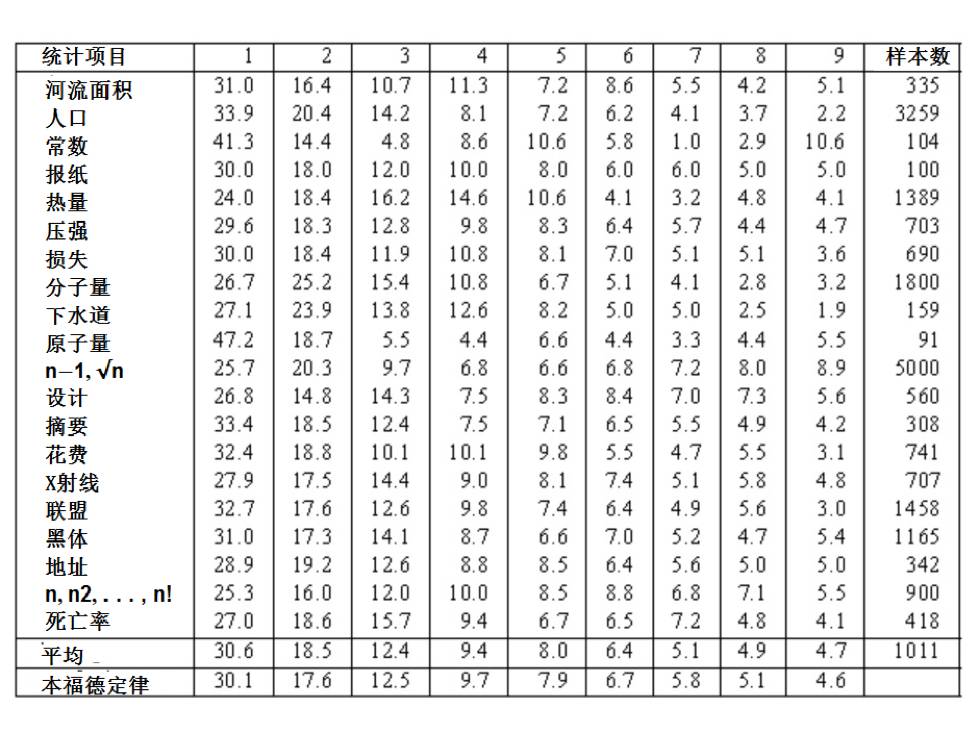
图2:本福特从大量数据中得到的首位数字概率表
本福特定律适用范围异常广泛,自然界和日常生活中获得的大多数数据都符合这个规律。尽管如此,此规律仍然受限于如下几个因素:
1、这些数据必须跨度足够大,样本数量足够多,数值大小相差几个数量级;
2、人为规则的数据不满足本福特定律,例如按照某种人为规则设计选定的电话号码、身份证号码、发票编号等等。为造假而人工修改过的实验数据、彩票上的随机数据也不符合本福特定律。
如何解释本福特定律?
尽管本福特和纽康都总结出了首位数字的对数规律,但并未给出证明,直到1995年美国学者Ted Hill才从理论上对该定律作出了解释,并进行了严谨的数学证明。虽然本福特定律在许多方面都得到了验证和应用,但对于这种数字奇异现象人们依旧是迷惑不解。到底应该如何直观理解本福特定律?为什么大多数数据的首位数字不是均匀分布而是对数分布的?
有人探求数“数”的方法,来直观解释本福特定律。他们的意思是说,当你计算数字时,顺序总是从1开始的,如果到9就终结的话,所有数字起首的机会都相同,但9之后的两位数10至19,以1起首的数则远多于其它数字。
我们可以用这种方法来理解街道号码 (地址) 一类的数据。一般来说,每条街道的号码都是从1算起,街道长度有限,号码排到某一个数就终止了。另一条街又有它自己的从1开始的号码排列,以此类推,1开头的号码是要多一些的。但这种解释也太不“数学”了!况且,这种理解无法说明另外一类数据为什么也符合本福特原则,如“物理常数”的集合、出生率、死亡率等,这些数据并不是从1开始计算到有限长度就截止的那种数据。
另一种解释是认为本福特定律的根源是由于数据的指数增长。指数增长的序列,数值小的时候增长较慢,由最初的数字1增长到另一个数字2,需要更多时间,所以出现率就更高了。
举个例子来说明这个道理:如果你有100美元的存款,年利率是10%,25年中,你每年的存款金额将是 (只保留了整数部分) :
100、110、121、133、146、161、177、195、214、236、259、285、314、345、380、418、459、505、556、612、673、740、814、895、985
这是一个指数增长的序列。在这组数据的25个数字中,首位数字为1的有8个 (32%) ;2的4个;3的3个……9的只有1个 (4%) 。这是因为从首位为1增加到首位为2,经过了更长的时间 (8年) ;从首位为2,只经过了4年就变成了首位为3;而首位为9的话,下一年又变成了1。所以,指数增长规律的数列的确符合本福特定律。
读者也许会有疑问:上面的数列选择从100开始,1打头的比较多,如果从别的数字开始,规律是否会改变呢?读者可以试验一下,得到的结果仍符合本福特法则。此外,你还可以将美元换算成人民币 (乘以6.7) ,得到的数据仍然会遵循本福特定律,这也说明本福特定律具有“尺度不变性”。
帮助侦破“数据造假”
由于大多数财务方面的数据都满足本福特定律,因此,在现实生活中,它可以用作检查财务数据是否造假!
美国华盛顿州曾侦破过一个当时最大的投资诈骗案,金额高达1亿美元。
诈骗主谋凯文·劳伦斯及其同伙以创办高技术含量的连锁健身俱乐部为名,向5000多个投资者筹集了大量资金。随后,他们挪用公款以作自身享乐。为了掩饰他们的不法行为,他们将资金在海外公司和银行间进行频繁转账,并且人为做假账,制造一种生意兴隆的错觉。
所幸,当时有一位名为Darrell Dorrell的会计师感觉不对头,他将70000多个与支票和汇款有关的数据收集起来,将这些数据首位数字发生的概率与本福特定律相比较,发现这些数据无法通过本福特定律的检验。最后经过了3年的司法调查,终于拆穿了这个投资骗局,2002年,劳伦斯被判20年牢狱。
2001年,美国最大的能源交易商安然公司 (Enron Corporation) 宣布破产,并传出公司高层管理人员涉嫌做假账的传闻。据传,安然高层改动过财务数据,因而他们所公布的2001-2002年每股盈利数据不符合本福特定律 。此外,本福特定律也被用于股票市场分析、检验选举投票欺诈行为等。
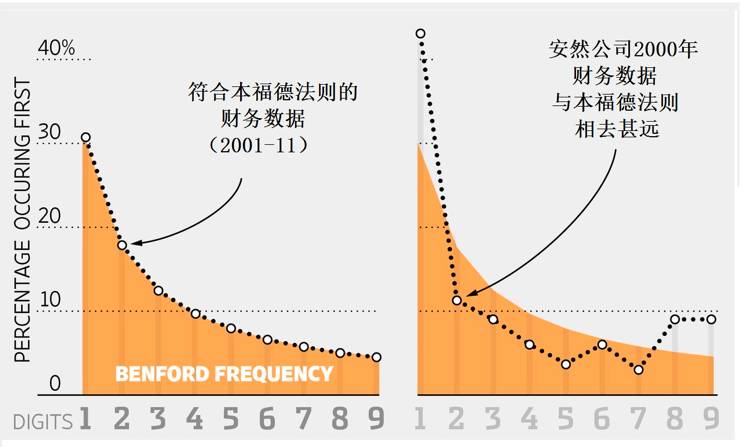
图3:安然公司数据vs本福特定律(图片来源: The wall street journal )
本福特定律适用场景
1、通过多个数据集运算形成的。例如:应收账款=销售量*单价,应付账款=采购量*单价。
2、真实交易数据,交易量、重量等。
3、大数据量,可观测的数据越多可能越符合。例如:全年的交易数据。
4、符合下面规律的会计科目:当一组数字的平均数大于中位数,且偏差为正。例如:大部分的会计科目。
本福特定律不适用场景
1、数据集合是标志性的编号。例如:对账单号、发票号、邮政编码。
2、数字会受到人为影响。例如:商家营销手段,通常会把2000元的商品标价1999。
3、数据集合包含大量公司特定的数字。例如:用来记录100美元退款的账户。
4、数据集合设定有最大值、最小值的门槛。例如:某类资产必须大于多少金额才会被记录。

游客
20-04-19 20:01
如果一组数据,不同的统计口径,本福特的值不同,甚至差别很大,怎么办?
比如销售订单,按月、日、小时统计的成交额,本福特指数偏离度分别为:35%,16%,7%,怎么解读?

游客
20-04-05 17:04
应该是的,可以统计下试试

游客
20-04-04 23:54
那么,年龄以1为开头的人数占比也是30%吗?

游客
20-03-20 18:23
👍👍👍
本福特定律(第一数字定律)详解

BigData
会员积分:500
本福特定律在线测试,https://www.itshenji.com/benfute
本福特(Benford)定律又称第一数字定律,它是数字统计的一种内在规律,指所有自然随机变量,只要样本空间足够大,首位1-9的数字出现的概率在一定范围内具有稳定性,即以1开头的样本占样本总量的30.1%,以2开头的样本占样本总量的17.6%,而以9开头的样本始终只占5%左右(如下图)。
常用于检查各种数据是否有舞弊、造假。
举一个例子
某银行有1000多个储蓄账户,存款金额不等。这些数字的第一位 (非零) 有效数字可能是1到9之间的任何一个。现在,我们设想一下,在上千个存款数据中,第一位数字是1的概率有多大?
大部分人可能很快地回答:应该是1/9吧。因为从1到9,9个数字排在第一位的概率是相等的,每一个数字出现的概率都是1/9,大约11%左右。
这种看似十分正常的思维却与真实的规律相悖。
经研究发现,很多情况下,首位数字是1的概率要比靠直觉预料的11%大得多。数字越大,出现在第一位的概率就越小,数字9出现于第一位的概率只有4.5%左右。各个数字出现在首位的概率遵循图1左图所示的概率分布。从图中可以看出,首位数字为1的概率可达30.1030%,而首位数字为9的概率仅为4.5757%。
这就是本福特定律。

图1:本福特定律(首位数定律)
事实上,本福特定律的发现者并不是本福特,而是美国天文学家西蒙·纽康 (Simon Newcomb,1835 - 1909) 。
纽康在查阅对数表(常用对数编排而成的表格,用以计算)时发现了一个奇怪的现象:包含以1开头的数的那几页比其他页破烂得多,似乎表明计算所用的数值中,首位数是1的概率更高,因此他在1881年发表了一篇文章提到并分析了这个现象,但没有引起人们的注意,直到57年之后的1938年,本福特又重新发现这个现象。
说来令人奇怪,科学定律的发现有时候来自于一些毫不起眼、小得不能再小的现象,本福特的发现便是如此。“以1开头的数字比较多”,这也算是一个定律吗?
本福特发现这种现象不仅仅存在于对数表中,也存在于其它多种数据中,于是,本福特检查了大量数据而证实了这点。
本福特和纽康都从数据中总结出首位数字为n的概率公式是:
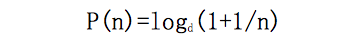
其中d取决于数据使用的进位制,对十进制数据而言,d=10。
随后,本福特收集并研究了20229个统计数据,包括河流面积、人口统计、分子及原子重量、物理常数等多种来源的资料,并分成20组。数据来源虽然千差万别,却基本上符合本福特定律,见图2所示的数据表。表中最后一行的数值,是根据本福特概率公式计算得到的每个数字出现于首位的概率,读者可以将它与真实数据相比较。

图2:本福特从大量数据中得到的首位数字概率表
本福特定律适用范围异常广泛,自然界和日常生活中获得的大多数数据都符合这个规律。尽管如此,此规律仍然受限于如下几个因素:
1、这些数据必须跨度足够大,样本数量足够多,数值大小相差几个数量级;
2、人为规则的数据不满足本福特定律,例如按照某种人为规则设计选定的电话号码、身份证号码、发票编号等等。为造假而人工修改过的实验数据、彩票上的随机数据也不符合本福特定律。
如何解释本福特定律?
尽管本福特和纽康都总结出了首位数字的对数规律,但并未给出证明,直到1995年美国学者Ted Hill才从理论上对该定律作出了解释,并进行了严谨的数学证明。虽然本福特定律在许多方面都得到了验证和应用,但对于这种数字奇异现象人们依旧是迷惑不解。到底应该如何直观理解本福特定律?为什么大多数数据的首位数字不是均匀分布而是对数分布的?
有人探求数“数”的方法,来直观解释本福特定律。他们的意思是说,当你计算数字时,顺序总是从1开始的,如果到9就终结的话,所有数字起首的机会都相同,但9之后的两位数10至19,以1起首的数则远多于其它数字。
我们可以用这种方法来理解街道号码 (地址) 一类的数据。一般来说,每条街道的号码都是从1算起,街道长度有限,号码排到某一个数就终止了。另一条街又有它自己的从1开始的号码排列,以此类推,1开头的号码是要多一些的。但这种解释也太不“数学”了!况且,这种理解无法说明另外一类数据为什么也符合本福特原则,如“物理常数”的集合、出生率、死亡率等,这些数据并不是从1开始计算到有限长度就截止的那种数据。
另一种解释是认为本福特定律的根源是由于数据的指数增长。指数增长的序列,数值小的时候增长较慢,由最初的数字1增长到另一个数字2,需要更多时间,所以出现率就更高了。
举个例子来说明这个道理:如果你有100美元的存款,年利率是10%,25年中,你每年的存款金额将是 (只保留了整数部分) :
100、110、121、133、146、161、177、195、214、236、259、285、314、345、380、418、459、505、556、612、673、740、814、895、985
这是一个指数增长的序列。在这组数据的25个数字中,首位数字为1的有8个 (32%) ;2的4个;3的3个……9的只有1个 (4%) 。这是因为从首位为1增加到首位为2,经过了更长的时间 (8年) ;从首位为2,只经过了4年就变成了首位为3;而首位为9的话,下一年又变成了1。所以,指数增长规律的数列的确符合本福特定律。
读者也许会有疑问:上面的数列选择从100开始,1打头的比较多,如果从别的数字开始,规律是否会改变呢?读者可以试验一下,得到的结果仍符合本福特法则。此外,你还可以将美元换算成人民币 (乘以6.7) ,得到的数据仍然会遵循本福特定律,这也说明本福特定律具有“尺度不变性”。
帮助侦破“数据造假”
由于大多数财务方面的数据都满足本福特定律,因此,在现实生活中,它可以用作检查财务数据是否造假!
美国华盛顿州曾侦破过一个当时最大的投资诈骗案,金额高达1亿美元。
诈骗主谋凯文·劳伦斯及其同伙以创办高技术含量的连锁健身俱乐部为名,向5000多个投资者筹集了大量资金。随后,他们挪用公款以作自身享乐。为了掩饰他们的不法行为,他们将资金在海外公司和银行间进行频繁转账,并且人为做假账,制造一种生意兴隆的错觉。
所幸,当时有一位名为Darrell Dorrell的会计师感觉不对头,他将70000多个与支票和汇款有关的数据收集起来,将这些数据首位数字发生的概率与本福特定律相比较,发现这些数据无法通过本福特定律的检验。最后经过了3年的司法调查,终于拆穿了这个投资骗局,2002年,劳伦斯被判20年牢狱。
2001年,美国最大的能源交易商安然公司 (Enron Corporation) 宣布破产,并传出公司高层管理人员涉嫌做假账的传闻。据传,安然高层改动过财务数据,因而他们所公布的2001-2002年每股盈利数据不符合本福特定律 。此外,本福特定律也被用于股票市场分析、检验选举投票欺诈行为等。

图3:安然公司数据vs本福特定律(图片来源: The wall street journal )
本福特定律适用场景
1、通过多个数据集运算形成的。例如:应收账款=销售量*单价,应付账款=采购量*单价。
2、真实交易数据,交易量、重量等。
3、大数据量,可观测的数据越多可能越符合。例如:全年的交易数据。
4、符合下面规律的会计科目:当一组数字的平均数大于中位数,且偏差为正。例如:大部分的会计科目。
本福特定律不适用场景
1、数据集合是标志性的编号。例如:对账单号、发票号、邮政编码。
2、数字会受到人为影响。例如:商家营销手段,通常会把2000元的商品标价1999。
3、数据集合包含大量公司特定的数字。例如:用来记录100美元退款的账户。
4、数据集合设定有最大值、最小值的门槛。例如:某类资产必须大于多少金额才会被记录。

19-11-26 10:07

27854

14
回复
如果一组数据,不同的统计口径,本福特的值不同,甚至差别很大,怎么办?
比如销售订单,按月、日、小时统计的成交额,本福特指数偏离度分别为:35%,16%,7%,怎么解读?

20-04-19 20:01
应该是的,可以统计下试试

20-04-05 17:04
那么,年龄以1为开头的人数占比也是30%吗?

20-04-04 23:54
👍👍👍

20-03-20 18:23
